Does it matter when it happens? Assessing whether quizzing at different timepoints in a course is predictive of final exam grades

Alice S. N. Kim¹, Mandy Frake-Mistak², Alecia Carolli¹ and Brad Jennings¹

¹Teaching and Learning Research In Action, Ontario, Canada
²Teaching Commons, York University, Ontario, Canada

Abstract

An important step towards promoting academic success is identifying students at risk of poor academic performance, particularly so they can be supported before they fall too far behind. In this study we investigated whether students’ grades on five quizzes that were distributed evenly throughout a course were differentially predictive of their grades on the final cumulative exam. Our focus was not on summative value of the quizzes, but rather how this information could be used to help inform more specific guidelines regarding when student performance should be a concern, and to provide insight for how to better individualize student support. The results of a regression analysis showed that students’ grades for the second, fourth, and fifth quiz were significant predictors of students’ performance on the final cumulative exam. Students’ grade on the first quiz reached borderline significance as a predictor of their grade on the final cumulative exam. Our findings suggest that students’ performance throughout various timepoints of a course is important to take into account for considerations about students' academic achievement. The implications of these findings include the use of frequent quizzing to identify students who would benefit most from additional, targeted academic support to improve the trajectory of their academic achievement. Additionally, students should be made aware of the relationship between their grades on quizzes to the final cumulative exam to help inform their decisions regarding individual academic planning and success.

Keywords

assessment, academic achievement, cumulative exam, knowledge retention

Introduction

Student performance on assessments helps communicate to both the student and course instructor what students know and what they are capable of (Kember & Ginns, 2012; McDowell, 2012). Moreover, it communicates to what extent students are achieving the intended learning outcomes for the course. Assessments can also be used for purposes beyond grading; they can function as a vehicle that allows students and the course instructor to determine if learning has taken place (Kember & Ginns, 2012; McDowell, 2012) and, further, to inform the teaching process (Ambrose et al., 2010). In this way, assessments can have both a summative and formative component.

Past work has shown that students’ grades on quizzes and midterms are predictive of their learning achievement in a course, as measured by their grades on a final cumulative exam (Azzi et al., 2015; Kim & Shakory, 2017; Landrum, 2007). For example, Winston et al. (2014) found that an exam administered two weeks into a course of study was predictive of whether students failed the course. Other studies have investigated midterm marks and whether they predict academic achievement in a course, and these studies demonstrate a positive relationship between students’ grades on formative assessments taking place midway through a course and their final grades (Azzi et al., 2015; Connor et al., 2005; Jensen & Barron, 2014).

Although past studies have investigated whether quizzes held early or midway through a course is predictive of students’ academic achievement, what remains unclear is whether quizzes that are completed by students at multiple, evenly distributed timepoints in the course (e.g., two vs. six weeks into a course) are equally predictive of students’ academic achievement in that course. This information could help inform more specific guidelines, based on data, regarding when student performance should be a concern. To our knowledge, this question has not been investigated in the literature. This study focuses on the predictive, formative value of these types of quizzes as opposed to their summative results. Further, this study aims to add to the literature by investigating the predictive utility of students’ grades on five quizzes that were evenly distributed throughout the duration of 12-week semester-long courses.

According to Harlen (2012), in general, assessment involves collection of data, judgement-making, and decision making about evidence that relates to the course goals being assessed. Formative assessment is used to gather information about students’ learning (Weston & McAlpine, 2004), and though grading may be involved, it need not be required. In contrast, summative assessment is used for the purpose of reporting and decision making about the learning process that has (or has not) taken place (Harlen, 2012).

Quizzes are an effective means of assessing how well students’ have learned course material (Sotola & Crede, 2020). In addition to being relatively easy to implement, low-stakes quizzes reduce anxiety around testing, motivate students to pay attention during lectures, and encourage class attendance (Singer-Freeman & Bastone, 2016). Past research has demonstrated that incorporating frequent low-stakes quizzes in a course decreases the odds of students failing the course, and that the use of quizzes was positively related to students' academic success in the course (Sotola & Crede, 2020). Past research has shown that students’ grades on a quiz that was held early on during the course, but not their grades on a quiz that was held halfway through the course, was predictive of their grade on the final cumulative exam (Kim & Shakory, 2017). In the present study, we investigated whether low-stake quizzes completed by students throughout a course (every second class) are differentially predictive of their grades on the final cumulative exam.

Our study took place in the context of a large, lecture-style Psychology course that was instructed at a large North American university. Students in two Psychology courses taught by the same instructor completed five quizzes that were held every second class, starting from the third class of the course (the five quizzes were held on the third, fifth, seventh, ninth, and 11th class of a 12-class course). Based on past work demonstrating that students’ grades on a quiz that was held early on during the course, but not their grades on a quiz that was held halfway through the course, was predictive of their grade on the final cumulative exam (Kim & Shakory, 2017), we hypothesized that students’ grades on the first two out of five quizzes would be predictive of their final cumulative exam grades but that students’ grades on the third and fourth quizzes would not be predictive of final exam grades. We are not aware of any studies that could serve as a basis for a hypothesis about whether the fifth quiz in the course would be predictive of students’ grades on a final cumulative exam, thus we took an exploratory approach for this analysis.

Method

Participants

All students who participated in the study were enrolled in a second- or third-year Psychology course at a large North American university. The courses were distinct and covered different topics. The second-year course was on cognition, while the third-year course was on the biological basis of behaviour. Both courses were taught by the same instructor and were included amongst groups of courses that students had to choose from for credits that counted towards their degrees. Students were invited to participate in the study after the final marks for their courses were submitted to the university. All students who participated in the study provided consent to have their data from the course included in the study, following the procedures approved by the Human Participants Review Sub-Committee, York University’s Research Ethics Board. Out of 469 students who completed the courses, 66 participated in the study (41 students from the third-year course, and 25 students from the second-year course). Of the 66 participants included in the study, 50 self-identified as being female and 16 self-identified as being male. The mean age of the students was 21.59 years (18 to 30 years; SD = 3.47 years). There was consistency in difficulty, duration, and length between quizzes in both courses and semesters and the same course instructor taught both courses.

Materials

In-class quizzes

The quiz questions were selected or designed by the course instructor to help prepare students for the final cumulative exam. Some were curated from a question bank provided by the publisher of the textbook used in the courses based on an instructor review of the learning outcomes and course materials. Other questions were edited versions from the publisher’s resources, modified to reflect the course concepts and content more accurately. Finally, quiz questions were also created by the instructor with a particular lens on capturing the concepts and content from the lectures.

The format for each of the quizzes consisted of multiple-choice and short answer questions which varied among quizzes. Quizzes for students in the second-year course consisted of 22-24 multiple-choice questions per quiz. Students in the third-year course were presented with a mix of approximately 18 multiple-choice questions and 5-6 short answer questions per quiz. The quizzes were paper-based, and the students wrote the quizzes during class time. The instructor provided clear instructions about how a student could achieve full marks or partial marks for short answer responses. The quizzes were marked by teaching assistants and the course instructor. The course instructor checked a random sample of students’ quizzes to ensure that there was consistency and accuracy of marking and found 100% agreement with the marks allotted by the teaching assistants. The high level of agreement between the course instructor and teaching assistants’ marking was attributed to a combination of conscientious marking by teaching assistants and the high level of detail provided in the answer key created by the course instructor.

The quizzes were not cumulative; instead, each quiz covered different components of the course material. Students received their grades for each quiz as a percentage score. Students received their grade on the quiz after the team completed their grading. Students were provided with their results prior to the next quiz, and, in the case of the last quiz, prior to the final exam. The questions were taken up during class and students had the option of reaching out to the instructor or their assigned teaching assistant for further clarification.

Exams

The final exams were cumulative and consisted of multiple-choice and short answer questions. Like the in-class quizzes, the final exam consisted of multiple-choice and short answer questions that required students to retrieve the correct information from memory and to apply course material. In the second-year course, there were 110 multiple-choice questions and 10 short answer questions. In the third-year course, there were 84 multiple-choice questions and 16 short answer questions. As with the quizzes, the exams were marked by teaching assistants and the course instructor. The course instructor checked a random sample of exams to ensure the teaching assistants were marking the exams according to the exam rubric. Students had three hours to complete the exams, and overall exam scores were calculated in the form of a percentage.

Procedure

The third-year Psychology course was offered in both the summer and fall sessions. The summer session consisted of two 3-hour lectures per week, with each lecture held on a different day of the week (14 students), whereas the fall semester consisted of one 3-hour lecture per week (27 students). The second-year Psychology course was offered in the fall session and consisted of one 3-hour class period per week. Both Psychology courses followed the same evaluation breakdown; students had the opportunity to complete five quizzes, and each quiz assessed students on material covered in the previous two lectures. A quiz was held every second class, thus students in the summer session completed a quiz each week, whereas students in the fall and winter sessions completed a quiz every second week. All students were notified at the beginning of the course, through class announcements and the course syllabus, that the instructor would use their best three quiz marks, out of five quizzes given across the term, to calculate 50% of their final mark in the course. Therefore, each quiz was worth 16.67% of their final grade in the course. The final cumulative exam would be worth 40% of their final mark with the remaining 10% of the students’ final marks allocated to class participation.

Analyses

An analysis of variance (ANOVA) was conducted on students' final exam scores to investigate whether there was a significant difference in final exam scores for students enrolled in the two courses; a significant finding may suggest the courses and/or the students enrolled in the two courses were very different and perhaps incomparable. An ANOVA was also conducted to check whether there was a significant difference in students’ final exam scores for the summer and fall offerings of the third-year Psychology course. A regression analysis was conducted to assess whether the five bi-weekly quizzes distributed throughout the courses were predictive of students’ performance on the final cumulative exam.

Results

An analysis of standard residuals reveals that the data did not contain any outliers (Std. residual min = -2.132, residual max = 2.023). When the assumption of collinearity was tested, the result demonstrated that the multicollinearity was not a concern (Quiz 1, tolerance = .924, VIF = 1.082; Quiz 2, tolerance = .864, VIF = 1.157; Quiz 3, tolerance = .927,
VIF = 1.078; Quiz 4, tolerance = .919, VIF = 1.089; Quiz 5, tolerance = .954, VIF= 1.049). The data also met the assumption of independent errors (Durbin-Watson value= 1.558). The histogram of standardized residuals showed that the data contained approximately normally distributed errors, as did the normal P-P plot of standardized residuals, which showed points that were close to being on the line. The scatterplot of standardized predicted values indicated that the data met the assumptions of homogeneity of variance and linearity. The data also met the assumption of nonzero variances (Quiz 1, variance = 677.617; Quiz 2, variance = 867.695; Quiz 3, variance = 824.969; Quiz 4 variance = 962.113; Quiz 5 variance = 685.421; final exam variance = 183.638).

ANOVA

The results of the ANOVAs did not reveal a significant difference in final exam scores between the two courses (M = 80.959, SD = 12.220 and M = 76.719, SD = 14.207 respectively; F(1, 64) = 1.534, p = .220), nor a significant difference in final exam scores between the summer and fall offerings of the third-year course (M = 75.697, SD = 13.642 and M = 77.248, SD = 14.717 respectively; F(1, 39) = .107, p = .745)

Multiple regression analysis

A multiple linear regression was calculated to predict students’ scores on a cumulative final exam based on scores on each of five quizzes that students were given throughout the course. Table 1 contains descriptive statistics for each of the five quizzes and the final exam grades. Figure 1 shows violin plots for each of the five quizzes.

Table 1. Minimums, maximums, means, and standard deviations for quizzes and final exam as percentages.

Assessment	Min	Max	Mean	SD
Quiz 1	19.86	97.80	57.64	26.03
Quiz 2	0	100.00	69.38	29.46
Quiz 3	0	100.00	73.91	28.72
Quiz 4	0	100.00	67.64	31.02
Quiz 5	0	100.00	72.27	26.18
Final Exam	47.80	98.70	78.32	13.55

Note. Min = minimum, Max = maximum, SD = standard deviation

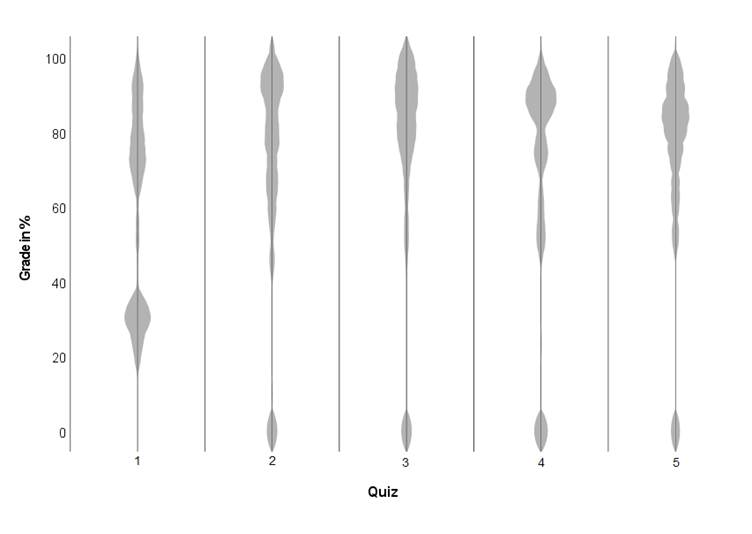
Figure 1. Violin plots of students’ grades for each of the five quizzes.

Using the enter method, a significant regression equation was found, F(5, 60) = 5.629,
p < 001 with an R2 of .319. Participants’ predicted scores on the final cumulative exam is equal to 40.073 + .111 (Quiz 1) + .110 (Quiz 2) + .051 (Quiz 3) + .157 (Quiz 4) + .136 (Quiz 5), where scores on all quizzes are measured in percentage. Students’ grades for the second (β = .239, t(60) = 2.084, p = .041), fourth (β = .359, t(60) = 3.231, p = .002), and fifth quiz (β = .264, t(60) = 2.416, p = .019) were significant (p < .05) predictors of students’ performance on the final cumulative exam. It is also worth noting that students’ grade on the first quiz reached borderline significance as a predictor of their grade on the final cumulative exam (β = .212, t(60) = 1.916, p = .060). In contrast, students’ grade on the third quiz (β = .109, t(60) = 0.982, p = .330) was not found to be a significant predictor of students’ performance on the final cumulative exam. Participants’ predicted cumulative exam scores increased by .111, .110, .157, and .136 for each percentage point of the first, second, fourth, and fifth quiz, respectively.

Discussion

Our results show that students’ grades on quizzes that were held on the fifth, ninth, and 11th class of a 12-class course were significant predictors of their performance on the final cumulative exam. It is also worth mentioning that students’ grade on the first quiz, which was held on the third day of class, reached borderline significance (p=.06) as a predictor of their grade on the final cumulative exam. Moreover, the quizzes that were shown to be significantly predictive of students’ performance on the final cumulative exam did not vary dramatically in terms of their predictive strength, with coefficients ranging from .110 to .157. Thus, our findings suggest that students’ performance throughout the entire course, except perhaps midway through, is important to take into account for considerations about students' academic achievement.

One of the main implications of these findings is that students’ performance on quizzes held as early as the third and fifth class (corresponding to the first and second quizzes, respectively) of a course can be used as a practical means of identifying students who may benefit most from additional academic support. At-risk students would likely benefit more from individualized and targeted academic support and resources based on their known needs, particularly if these needs were recognized earlier than later in the course before they fall too far behind. Moreover, knowledge of the relationship between students’ performance on quizzes held early during a course and their performance on the final exam may also help students to assess their viability of staying in the course and completing it successfully. Such information is important as it would allow students to make an informed choice about whether or not they want to drop the course or proceed to complete it; beyond the consequences of a low or failing grade to their academic record, in the North American context that we are operating in, students may wish to drop a course within the permitted add/drop period that would allow for them to receive a partial refund that they could then use to register in the course, or an alternative, at a later time when they are more likely to be successful. Additionally, course instructors may wish to review with their students the material included in quizzes that students performed poorly on, particularly if these quizzes were administered at the beginning or towards the end of the course, as our results suggest that students’ performance on these quizzes are predictive of their performance on the final cumulative exam. This finding suggests that, overall, students do not achieve mastery of course material based on feedback received from prior assessments alone, and that they may benefit from an explicit, guided review of where they went wrong on the assessment to help enhance their learning of the course material.

Our results are consistent with past research on the relationship between students’ grades on assessments held early on during a course and their overall achievement in the course (e.g., Nowakowski, 2006; Winston et al., 2014). However, our findings contrast past research demonstrating a positive relationship between students’ grades on assessments held midway through a course and their final grades (Azzi et al., 2015; Connor et al., 2006; Jensen & Barron, 2014). Instead, we found that students’ grades on a low-stakes quiz held midway through the term, at a time when students may prioritize other high-stakes assignments, were not predictive of their final exam grades. This may be due to how much weight the quizzes in the present study contributed to students’ final grades in the course; only the top three out of five quiz grades were used to derive students’ final grades in the course. In contrast, Azzi et al. (2015) found a significant correlation between students’ scores on a midterm that was worth 30% of students’ final mark for the course and the final cumulative exam. Due to the high-stakes nature of the midterm, students may have been more motivated to prepare as best as possible for it. In the context of the present study, students’ top three quiz marks were used to calculate their final grade and it is possible that their grade for the third quiz was not one of their top three quiz marks even though they did not make an explicit decision that this quiz would not be used towards their final grade. Future research should investigate further the potential impact of the weight of an assessment, in addition to when the assessment is held, on its relation to students’ overall achievement in a course.

Conclusion

The results of the present study suggest that students’ grades for quizzes held as early as the third and fifth class of a 12-class course can help identify which students would benefit most from additional academic support. Students’ grades on quizzes that were held on the ninth and 11th class also significantly predicted their performance on the final cumulative exam. For course instructors, the potential implications of our findings include using students’ grades on quizzes throughout the course to identify which students would benefit most from additional academic support, improving the trajectory of their academic achievement in the course. Similarly, if students are aware that their grades on assessments that are held as early as the third and fifth class are predictive of their final cumulative exam marks, they could use their marks on these assessments to inform their decisions relevant to individual academic planning and success. Course instructors may also wish to review with their students the material included in quizzes that students performed poorly on, specifically if these quizzes were administered at the beginning or towards the end of the course. Future research should investigate further how the relationship between students’ assessments and their final cumulative exam marks and overall academic success may differ based on a variety of factors, including the types of assessment (e.g., quizzes, reports, and presentations), as well as individual factors that differ across students (e.g., motivation, ability, and effort).

References

Ambrose, S. A., Bridges, M. W., DiPietro, M., Lovett, M. C., & Norman, M. K. (2010). How learning works: Seven research-based principles for smart teaching. John Wiley & Sons.

Azzi, A. J., Ramnanan, C. J., Smith, J., Dionne, É., & Jalali, A. (2015). To quiz or not to quiz: Formative tests help detect students at risk of failing the clinical anatomy course. Anatomical Sciences Education, 8(5), 413–420. http://dx.doi.org/10.1002/ase.1488

Connor, J., Franko, J., & Wambach, C. (2005). A brief report: The relationship between mid-semester grades and final grades. University of Minnesota.

Harlen, W. (2012). On the relationship between assessment for formative and summative purposes. In J. Gardner (Ed.), Assessment and learning (pp. 87-102). SAGE Publications Ltd. https://doi.org/10.4135/9781446250808.n6

Jensen, P. A., & Barron, J. N. (2014). Midterm and first-exam grades predict final grades in biology courses. Journal of College Science Teaching, 44(2), 82– 89. https://doi.org/10.2505/4/jcst14_044_02_82

Kember, D., & Ginns, P. (2012). Evaluating teaching and learning: A practical handbook for colleges, universities and the scholarship of teaching. Routledge. https://doi.org/10.4324/9780203817575

Kim, A. S. N., & Sharkory, S. (2017). Early, but not intermediate, evaluative feedback predicts cumulative exam scores in large lecture-style post-secondary education classrooms. Scholarship of Teaching and Learning in Psychology, 3(2), 141–150. https://doi.org/10.1037/stl0000086

Landrum, R. E. (2007). Introductory psychology student performance: Weekly quizzes followed by a cumulative final exam. Teaching of Psychology, 34(3), 177-180. https://doi.org/10.1080/00986280701498566

McDowell, L. (2012). Assessment for learning. In L. Clouder, C. Broughan, S. Jewell, & G. Steventon, (Eds.), Improving student engagement and development through assessment: Theory and practice in higher education (pp. 73-85). Routledge.

Nowakowski, J. (2006). An evaluation of the relationship between early assessment grades and final grades. College Student Journal, 40(3), 557-561.

Singer-Freeman, K., & Bastone, L. (2016). Pedagogical choices make large classes feel small (Occasional Paper No. 27). National Institute for Learning Outcomes Assessment. https://www.learningoutcomesassessment.org/wp-content/uploads/2019/02/OccasionalPaper27.pdf

Sotola, L. K., & Crede, M. (2020). Regarding class quizzes: A meta-analytic synthesis of studies on the relationship between frequent low-stakes testing and class performance. Educational Psychology Review, 33, 407–426. https://doi.org/10.1007/s10648-020-09563-9

Weston, C., & McAlpine, L. (Eds.) (2004). Evaluating student learning. In Rethinking teaching in higher education: From a course design workshop to a faculty development framework (pp. 95-115). Stylus. https://doi.org/10.4324/9781003446859-8

Winston, K. A., Van der Vleuten, C. P. M., & Scherpbier, A. J. J. A. (2014). Prediction and prevention of failure: An early intervention to assist at-risk medical students. Medical Teacher, 36(1), 25-31. https://doi.org/10.3109/0142159X.2013.836270